Calculus Vs algebra:-

-By K Sreram

This article was first written on 2013

Introduction:-

This article was written to show the difference between arithmetic algebra and calculus. Differentiation and integration is far different from arithmetic algebra (though arithmetic algebra is used to represent the process of differentiation, differentiated equations, integrated equations or expressions) because, arithmetic algebra does not support the results provided by differentiation or integration process. Arithmetic algebra shows that the result provided by differentiation or integration process is approximated and the error will never be zero; but calculus says exact values.

I have proved all this in this article. This article also shows us what actually calculus is and how to apply them practically. Differential and integral calculus is a modification done to the mathematics at the time when arithmetic (and some geometric) algebra was prominent. It defines a wrong result (according to the ordinary algebra) to be correct (with proper proofs).

Differentiation: a brief recollection:-

Differentiation has many view points of its own. If we talk about application of differentiation, we represent many different characteristics of differentiation. Let me provide the mathematical definition instead of defining it statement vice because many statements can be obtained from the definition:-

 ; This definition can be interpreted in several ways (as I mentioned before) but let me tell you about two basic ways:-

1. where tangent of the slope as a function of x .
2. ; Then represents the area of the enclosed surface between the curve and x-axis, along its limits.

1. F’(x) as tangent:-

                                                       Fig 1.

From fig1, tangent of the slope across limits will be (as).

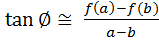2. F’(x) as y-axis:-

            Fig2.

Here,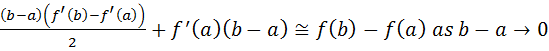

................... (1)

So again,

.................. (2)

is almost same as f’(b).

So if we take the y-axis to be f’(x) and x-axis to be x itself to get a curve, then the area of the curve with respect to x axis is f(x).

Note: - I have used approximately equal to symbol while representing it in (1) but in (2) I have used the equal to symbol. This is because, while representing algebraically, we have to be exact.

Differential calculus has many other uses such as, finding the minima & maxima of continues functions, to find whether the function is increasing or decreasing, etc.

Integration is the inverse of what was seen above; i.e..,

, delta x is considered as unity in this summation (i.e.., ).

Calculus: as a new idea:-

let there be a function f’(x) such that there exist another function f(x) such that f’(x) represent the tangent of each small line segment across the curve f(x). While integrating, for each value of ‘x’ in ‘f(x)’, there is a line segment of magnitude: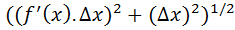. So the integrated value, obtained after integration will be very close to f(x). But general idea of algebra would say that it is not f(x) itself, calculus modifies this statement with relevant evidence and says that the integrated value is f(x). It is actually a postulate that does not have an origin from basic algebra. Quantities such as tangent exist only for line shapes, not for shapes that have a curve. But for us to compute the area from a function, we consider curves to be built up of infinitely small vectors across the curve.  

If (f’(x), x) is plotted in a plain graph, then, f(x) is the area across the slope of f’(x) (considering 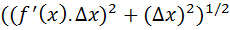to be the largest line segment superimposing the curve at the point x completely).   .

From the above equation f(b)-f(a) will be (if a & b are the limits),

    =>    

=>

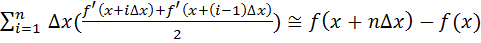
................ (3)

Here.

If we write an expression,, it means that there exist a value n such that, 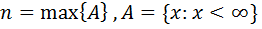; n has both the characteristics of as it is considered very large but not infinity. The difference between the characteristic of infinity and n approaches infinity is,

1/n is not absolute zero and it contributes to the magnitude of a summation of 1/n significantly only if it’s summed up to a very large value such as n or close to infinity (1/n is generally considered to be zero).

But for 1/infinity, there is no magnitude at all and summation of 1/infinity to a large value such as infinity will always be undefined (1/infinity is always considered to be zero no matter what value is multiplied to it).

Let me prove that, though algebraically, n->infinity is a real number, it can be considered to be infinity itself:-

Let’s consider we use a very large length measuring scale which has its maximum reading very large; unless it’s not infinity, there should always be a value several times larger than its maximum reading. So for n-> infinity, for x < L/n (L is the length of the scale), x is zero according to the measuring scale. If we choose another measuring scale with its maximum reading (but same units of measurements) much larger than the previous example, then n value can be chosen much larger such that L’/n is also read as zero in the newly considered scale (L’ is the second scale’s length). Unless the magnitude of L’ is real number, there will always exist a value n that is much larger than the magnitude of L’.  

In the equation,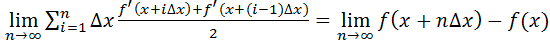, delta x is same as 1/n. hence. and 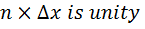or in some cases it can be a real number not equal to 1 as in the case above.

In the mathematical definition of differentiation: after the simplification of this expression until there is no delta x in the denominator, then we are free to substitute any value for delta x much small than the measuring unit or the least significant value of the system; ultimately, we are free to substitute zero for delta x. We cannot substitute a value to delta x such that it provides a significant value on multiplying it with a value smaller than the maximum value of the system.

Calculus freely shows that 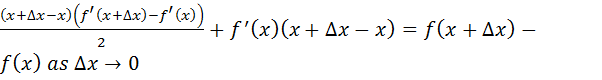instead of showing an approximation symbol relating LHS and RHS as in (1) because, we are free to consider delta-x much smaller such that it exceeds the system’s significance level in all cases so ultimately, its true for all real systems though algebraically its only approximated and delta-x is not zero.

Alternate proof:-

Let 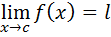be true;................. (4)

Then by definition, 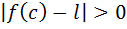..................(5)

Let then 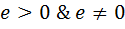also

), but hence, and so and (4) is wrong. But calculus defines it to be one hundred percent true; it cannot be proved true using normal arithmetic algebra but it can be proved to make no difference, though its wrong (this is so because though its correct it cannot be proved correct using algebra). Note that area of a curved surface cannot be estimated because of the reason that “squares” cannot be fitted along slopes.

Let’s define a constant ‘a’ as,; lets also define R’s minimum value possible as Then ‘e’ should be lesser than ; this is not true algebraically as, if then ‘e’ should take a value ‘a’ cannot take. But trying to overcome this problem, we write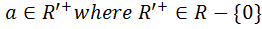. Then we get which is wrong according to the definition (5). So here we redefine the nature of e saying, both the definitions are correct ((5)and e<a, a is in R); we are able to do this as, if there exist a variable e with such a nature then e keeps getting close to zero but not zero. A value so small can be considered as zero. i.e.., if   is true, then e>0 (from (5)) and e<a is true so for any limiting value ‘a’ close to zero, and for all values of a, e can be considered to be zero. But still, as e>0, e/e=1.

A letter to the reader:-

                    Dear reader,

Mathematics is not a subject that can be mastered by learning the methods and proofs to solve different problems; it is a kind of subject in which we translate the nature in a way we can deeply understand and analyse it. A subject such as maths is just a different view of everything around as, and we can analyse the things around us just by analysing the equations we write. We can only understand and learn maths by feeling the natural laws and quantizing them; it will be an adventurous process to learn maths. Remember; when I say learning maths, I don’t refer to bookworms, but I refer to exploring the subject ourselves and not by reading a book and practising problems.

No mathematical from is universal, and the attempt to make it universal goes on forever! Remember, thinking different is seeing things in a different way and it can be wrong for many times before its correct; never underestimate anyone who thinks differently and is wrong most of the time, because for each mistake they make they learn something which no one can learn.

-K Sreram. 

   copyright © 2015 K Sreram, All rights reserved