Maxwell’s distribution law analysis:
This document is composed by K Sreram (a CSE student)
This derivation proceeds with a pre-defined assumption that if system of molecules exist relatively inert with each other and having a constant free energy, then the environmental conditions surrounding a unit within the system does not depend on the energy state of itself. This shows that the rise or fall of the energy of a molecule in a system of gas molecules (maintained at a particular temperature) does not depend upon the energy it possesses.
This assumption will contradict the laws governing the transfer of heat energy from one system of molecules to the other. But it could still be considered to hold good as this assumption does not contradict the law of conservation of energy as the decrease in the energy content of one molecule results in the increase in energy of the other molecule. Also, the laws of thermodynamics (other than the law of conservation of energy) is proposed based on a system and not individual particles.
But Maxwell’s distribution law talks about the most probable distribution of certain amount of energy within a system while the average amount of energy remains constant over time (when the system has acquired thermal equilibrium). So the above mentioned assumption is necessary and obvious as the converse (the environmental condition does depend on the energy level of the particle taken into consideration) leads to the conclusion that the system has not acquired thermal equilibrium and a certain reaction (chemical change) takes place (note that no external energy is supplied).
Because, the probability of a selected particle from the system to lose or gain a particular amount of energy does not depend upon the energy level of that particle, it is safe to write:
Let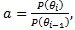 then
then . Let there be
. Let there be 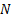 number of particles in the system, then the total number of particles with energy level
number of particles in the system, then the total number of particles with energy level . But if we want this expression as the function of the particles with ground energy level, then the expression can be modified as,
. But if we want this expression as the function of the particles with ground energy level, then the expression can be modified as,
(2)
|
We can write the expression of  as,
as,
(3)
|
(4)
|
Or,
(5)
| ||
(6)
|
The expression for 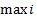
 can be written in terms of the total energy of the system and the least possible energy level as,
can be written in terms of the total energy of the system and the least possible energy level as,  which on a general scale is assumed to tend to infinite. Because
which on a general scale is assumed to tend to infinite. Because 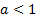 for all cases, the series
for all cases, the series  is convergent and from our previous definition,
is convergent and from our previous definition,  we can say that that series is a summation of probability of a selected particle from
we can say that that series is a summation of probability of a selected particle from 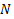 number of such particles in a system to have the energy state
number of such particles in a system to have the energy state  . Let’s define
. Let’s define 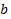 as the probability of the selected particle to be in the least possible energy state. Since
as the probability of the selected particle to be in the least possible energy state. Since , we get
, we get  and (6) modifies to
and (6) modifies to
(7)
|
Determining the relation between 
 and the energy of the particle in the system completes the derivation. We can treat
and the energy of the particle in the system completes the derivation. We can treat  as an infinite series so we can write,
as an infinite series so we can write,
(8)
| ||
(9)
|
For mathematical formulations based on series used here, refer to apex 1. Now energy can be taken into account. For maintaining the generality let  be the ground state energy of the system. And each energy state is said to be varied by units of
be the ground state energy of the system. And each energy state is said to be varied by units of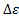 . So the expression for the net energy of the system can be written as,
. So the expression for the net energy of the system can be written as,
(10)
| ||
Or,
| ||
On substituting for
|
(11)
|
Assuming  to be the internal energy of the system before supplying energy, then we can write
to be the internal energy of the system before supplying energy, then we can write , where
, where 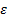 the free energy of the system, and it’s this energy which remains constant after attaining thermal equilibrium with the environment which is maintained at a constant temperature.
the free energy of the system, and it’s this energy which remains constant after attaining thermal equilibrium with the environment which is maintained at a constant temperature.
(11) can be written as,
| ||
Or,
| ||
Let,
| ||
Then we can write,
| ||
(12)
|
The equation (12) is just a simple quadratic equations with two possible solutions for . From the beginning, this derivation is based on the fact that each particle with a particular amount of energy and the entire system in the state of thermal equilibrium is considered to be treated “fare” by providing the same environmental condition to each of them. So the probability of gaining
. From the beginning, this derivation is based on the fact that each particle with a particular amount of energy and the entire system in the state of thermal equilibrium is considered to be treated “fare” by providing the same environmental condition to each of them. So the probability of gaining  amount of energy is determined by the same probability function for all particles of different energy levels because of the fact that though the system experiences a loss of energy through radiation or any other phenomena, there is an equal amount of energy supplied to the system (by definition). So that ensures that the environment experienced by each particle in the system is the same.
amount of energy is determined by the same probability function for all particles of different energy levels because of the fact that though the system experiences a loss of energy through radiation or any other phenomena, there is an equal amount of energy supplied to the system (by definition). So that ensures that the environment experienced by each particle in the system is the same.
Now from (12), we have,
This result can be obtained by using quadratic root formula and completing the expression of the solution. The solution that is negative is omitted. The steps for computing the final solution of  and the process of substituting it in the
and the process of substituting it in the 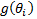 expression is omitted here.
expression is omitted here.
Appendix 1:
Derivation of the formula for the geometrically progressive series.
Let  be the sum of the geometric progression
be the sum of the geometric progression . Then
. Then . Or
. Or  can be written as
can be written as . On computing
. On computing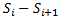 we get
we get . Or we can write,
. Or we can write,
Or
|
For the infinite limiting case, we have, 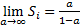 if
if  and the limit is divergent for all values of
and the limit is divergent for all values of  greater than 1.
greater than 1.
Derivation of the formula for the sum of the series .
.
Again, let  represent the series and obtain the difference
represent the series and obtain the difference 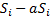 which can be written as,
which can be written as,
Or,
| ||
Or,
| ||
Now on limiting to infinity we get,
|
About my blog
copyright (c) 2015 K Sreram, all rights reserved.

Awesome posts my boy.........truly this much of knowledge in 1st year no in 1st semester is mind blowing.......
ReplyDelete