The mega confusion about infinity clarified!
By K Sreram
An answer to my friend’s question posted in that group.
The most “complicated number” in mathematics is infinity. It’s not because it’s extremely large or indeterminable or something, it’s because it inherits unique properties which other numbers in the set of real numbers don’t possess. And your question (refer to the group for the asked question) is about infinity that is not actually infinity!!! How am I saying that? It’s simple: you have been talking about numbers that nearly approach infinity (which anyone might say is logically impossible. Imagine a number as large as . There is always a number greater than that number (
. There is always a number greater than that number (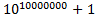 ). But we can say
). But we can say 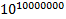 is almost equal to
is almost equal to  because, beside such a large number 1 has no value! So we can never make a number approach infinity and we always say
because, beside such a large number 1 has no value! So we can never make a number approach infinity and we always say 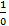 as purely undefined or it does not refer to anything at all.
as purely undefined or it does not refer to anything at all.
But that’s not the same infinity (it is not ) you have been talking about in that question. Before confusing you further, let me put forward the actual definition of the infinity you have been talking about: a number
) you have been talking about in that question. Before confusing you further, let me put forward the actual definition of the infinity you have been talking about: a number 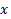 that is always greater than the limiting number
that is always greater than the limiting number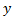 . Note that
. Note that 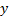 is a perfect number (i.e., belongs to the set of real numbers). So we can write
is a perfect number (i.e., belongs to the set of real numbers). So we can write  and let’s assume that the value of
and let’s assume that the value of  and
and  become extremely large but not infinity, then we have our
become extremely large but not infinity, then we have our  value which we are free to consider as infinity.
value which we are free to consider as infinity.
Note: in differential calculus and limits and any other subject involving these concepts, do not talk about the actual infinity but an extremely large and indeterminable number which exceeds the maximum limit of our measuring scale and which our measuring scale marks as: “unmeasurable large!”.
We can say that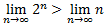 . Note that here we are not writing
. Note that here we are not writing  but instead we are writing
but instead we are writing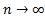 . The later expression is different from the former expression. The
. The later expression is different from the former expression. The  stands for “approaches” and does not stand for “is equal”.
stands for “approaches” and does not stand for “is equal”.
A little math:
Or we can write,
So we have one infinity 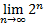 greater than the other infinity
greater than the other infinity .
.
Update:
There is one more thing I would like to add. There is an answer among people that fits their imagination and quenches their curiosity because they refuse to think further. They believe that even the absolute infinity can be subjected to be compared. But that’s not the case. Many of us say that 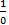 is infinity, but I wish to say
is infinity, but I wish to say  is plainly undefined if the zero in the denominator is an absolute zero and not infinity! Let’s say that there is an equation of some sort. Then we would have the LHS and the RHS with either an equal to sign or other arithmetic comparison symbol separating them. But what is the equation’s solution? It’s simple: on trying out all the possible numerical or expression substation to the present unknown symbol in the equation, the one(s) that satisfy the equation are chosen as the solution or the solution set. Remember the details of the order by which we substitute the symbol with the possible expression or the numerical value is not present in the equation. We may substitute random values until we get the correct solution. What does all this have to do with
is plainly undefined if the zero in the denominator is an absolute zero and not infinity! Let’s say that there is an equation of some sort. Then we would have the LHS and the RHS with either an equal to sign or other arithmetic comparison symbol separating them. But what is the equation’s solution? It’s simple: on trying out all the possible numerical or expression substation to the present unknown symbol in the equation, the one(s) that satisfy the equation are chosen as the solution or the solution set. Remember the details of the order by which we substitute the symbol with the possible expression or the numerical value is not present in the equation. We may substitute random values until we get the correct solution. What does all this have to do with ? Let me tell you: if the zero in the denominator is absolute zero, then there is no tendency for the zero to increase or decrease further (either go to the negative axis or the positive axis). Let’s write
? Let me tell you: if the zero in the denominator is absolute zero, then there is no tendency for the zero to increase or decrease further (either go to the negative axis or the positive axis). Let’s write  or we get
or we get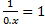 . Dose this even make sense? The solution for this equation is for some value of
. Dose this even make sense? The solution for this equation is for some value of  the value
the value  becomes one. How will this zero become one if it doesn’t have the tendency to move towards a value? Zero is nothing; it doesn’t have any value at all. How many ever times you add zero, it cannot become something because it doesn’t have the tendency to become something. Note that if there is a specific order by which we substitute values to
becomes one. How will this zero become one if it doesn’t have the tendency to move towards a value? Zero is nothing; it doesn’t have any value at all. How many ever times you add zero, it cannot become something because it doesn’t have the tendency to become something. Note that if there is a specific order by which we substitute values to 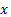 we might be able to say some answers. If the order is increasing (that is first we substitute 1 and then 2 and then 3 and so on) then our answer is infinity; and that is exactly what is represented by
we might be able to say some answers. If the order is increasing (that is first we substitute 1 and then 2 and then 3 and so on) then our answer is infinity; and that is exactly what is represented by . It says that
. It says that 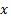 starts small and approaches infinity.
starts small and approaches infinity.
One more interesting fact about zero is that, it’s the origin of every dimension known. Let’s consider a one dimensional space coordinate. It has the zero in its center separating the negative and the positive regions. Now imagine another axis; this would make it 2 dimensional space. Again, zero is the meeting point for both the axis. Let’s now extend our imagination to a 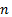 dimensional space. Zero, is now the meeting point of all the
dimensional space. Zero, is now the meeting point of all the 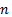 dimensions! So now if we are to multiply that zero by scalar quantity
dimensions! So now if we are to multiply that zero by scalar quantity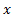 and if we are to say that the value of the product is non zero, then out of these
and if we are to say that the value of the product is non zero, then out of these  dimensions through which dimension should this product fall under? Note that zero is not a non-vector; it’s a vector. It’s a vector having all directions to move to. It’s like a bridge between higher dimensions.
dimensions through which dimension should this product fall under? Note that zero is not a non-vector; it’s a vector. It’s a vector having all directions to move to. It’s like a bridge between higher dimensions.
To put it shortly, 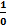 has no meaning.
has no meaning.
Summary:
The infinity used in many calculations that involve is not actual infinity but an expression that gives a number that can be treated as infinity while adding, subtracting with a finite value or while just writing down the result, but is treated as any other number while doing operations like multiplication, division, either with infinite numbers or finite numbers. In the given example, there are more number of ’s in the
’s in the  expansion than that single
expansion than that single  in the linear limit expression.
in the linear limit expression.

No comments:
Post a Comment